What Are Sphere, Cylinder, Axis, and Add Power in an Eyeglass Lens Prescription?
Sphere: The Basis of Your Prescription
The sphere component of a prescription indicates the degree of nearsightedness or farsightedness. It's expressed in diopters and determines the basic power of eyeglass lenses. A spherical cornea is perfectly round, and a spherical lens corrects vision by bending light uniformly in all directions. If you have a spherical error, your cornea's shape resembles a round ball, and the sphere value on a prescription counters this to sharpen vision.
Cylinder: Correcting Astigmatism
Astigmatism occurs when the cornea is shaped more like a football than a sphere, resulting in blurred or distorted vision. The cylinder value in the prescription addresses this by providing additional lens power in specific areas. It corrects the uneven curvature of the cornea, ensuring light focuses correctly on the retina.
Axis: Precision in Lens Positioning
Axis is crucial for astigmatism correction. It's a measurement in degrees, indicating the orientation of the cylinder power. The axis ensures the cylindrical correction aligns precisely with the astigmatic curve of your cornea, providing clear vision.
Add Power: Enhanced Reading Vision
For those with presbyopia, add power is an essential component. It represents the additional magnifying power needed for near tasks, like reading. This value is usually seen in bifocal or progressive lenses and helps with focusing on close objects.
FAQs: Common Questions About Prescriptions
- What Does a Negative or Positive Sphere Value Mean?
- Negative values indicate nearsightedness, while positive values suggest farsightedness.
- Can I Have a Prescription Without Cylinder and Axis?
- Yes, if you don't have astigmatism, your prescription may only include a sphere value.
- How Is Axis Determined?
- Through a refraction test conducted by your eye care professional.
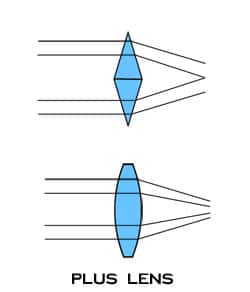
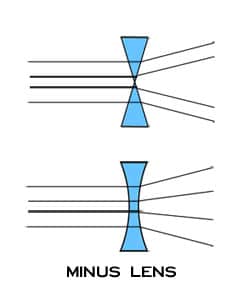
It can be helpful to think of very basic lens forms in terms of prisms. Recall, as light passes through a prism it is refracted toward the prism base. Minus lenses therefore resemble two prisms apex to apex spreading light rays outward as they pass through the lens, while plus lenses resemble two prisms base to base converging light rays as they pass through the lens.
Of course, most lenses are not comprised of angular prismatic surfaces but consist of curved surfaces. The most basic of these curves is a sphere. The curve on the surface of a spherical lens, if extrapolated in all directions, would form a ball or perfect sphere. The sphere would vary in size based on the steepness of the curve. A steeper, higher power curve would form a smaller sphere with a smaller radius, while a flatter, lower power curve would form a larger sphere with a larger radius.
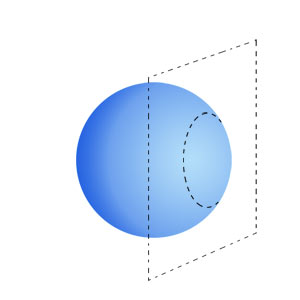
In addition to being described by their power or radius, spherical curves also have a direction. An inward curve is called concave, while an outward curve is called convex. Thinking back to the prism example, a minus lens that diverges light would require a concave spherical surface, while a plus lens that converges light would require a convex surface. Therefore, we use the minus (-) sign to denote concave curves, the plus (+) sign to denote convex curves, and the term "plano" to describe a flat or zero curve.
A lens has two curved surfaces of consequence to the vision of the wearer: the front surface and the back surface. Common lens shapes produced by an optical wholesale lab, based on front and back curves are described in the figure below.
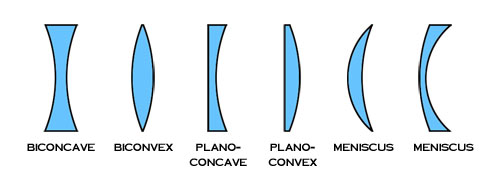
The corrective power of a lens is determined by adding the front curve to the back curve. This is expressed by the equation: F1 + F2 = FTotal. As you can see from this equation for any given corrective power, an infinite number of curve combinations may be used to achieve the same result.
Example:
+6.00 D + -2.00 D = +4.00 D
+4.00 D + 0.00 D (plano) = +4.00 D
+2.00 D + +2.00 D = +4.00 D
Practically speaking, the laboratory has a limited number of curve combinations with which to work. Lens blanks come from manufacturers with a limited selection of front curves, also known as base curves, with suggested power ranges for each. Furthermore, since aberrations occur as the eye moves away from the optical center of the lens, the lab will choose curves that minimize aberrations. Lenses with curves chosen to minimize aberrations are called "corrected curve" or "best form" lenses.
The following chart shows basic guidelines for selecting base curves to minimize peripheral aberrations.
| Sphere Power | Base Curve | |
| > +12.25 | +16.00 D | |
| +10.75 to +12.25 | +14.00 D | |
| +9.00 to +10.50 | +12.00 D | |
| +5.50 to +8.75 | +10.00 D | |
| +2.25 to +5.25 | +8.00 D | |
| -1.75 to +2.00 | +6.00 D | |
| -2.00 to -4.50 | +4.00 D | |
| -4.75 to -8.00 | +2.00 D | |
| -8.00 to -9.00 | +0.50 D | |
| < -9.00 | plano or minus | |
Remember, these are only guidelines for selecting base curves, there are typically many more factors involved in base curve selection including: manufacturer recommendations, frame selection, aesthetics, lens material, and patient history.
In addition to the spherical curve, many prescriptions call for a cylinder curve to correct for astigmatism. A cylinder curve is curved along a single axis and flat along the perpendicular axis. Furthermore, while the focus of a spherical curve is a single point, the focus of a cylinder curve is a line. The meridian along which there is no cylinder power in the lens and consequently the meridian of the cylindrical focus is the cylinder axis. The cylinder axis is expressed in degrees between 0 and 180.
Most prescriptions have some combination of spherical and cylinder curves. A lens that combines spherical and cylinder curves is called a compound lens or toric. The convention of the power cross helps conceptualize the compound lens. The power cross is a representation of the two major meridians of the lens surface. The simplest combination to visualize is a plano with +4.00 D cylinder.
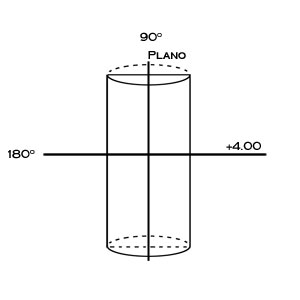
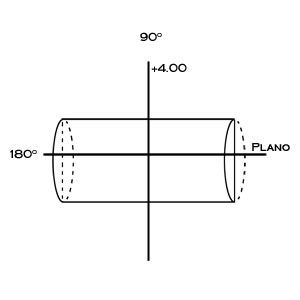
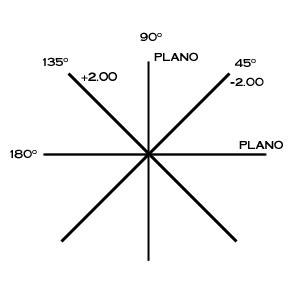
The above examples show the cylinder curve at right angles. Note how the power in the meridian of the cylinder axis is plano, while the power of the meridian perpendicular to the cylinder axis is +4.00 D. To fully understand the cylinder curve, however, it is important to consider the lens form at meridians other than 90º and 180º from the cylinder axis.
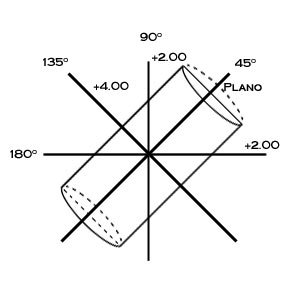
The figure above shows the +4.00 D cylinder curve at 45º. Note, the curves at the 90º and 180º are now +2.00 D and the +4.00 D curve is now at 135º. As the meridian is rotated away from the cylinder axis, the curve gradually changes from 0 to the full power of the cylinder curve (+4.00 D in this example) once the meridian is perpendicular to the cylinder axis. A simple equation can be used to determine the amount of cylinder power in any meridian: F = Fcyl*(SIN(Î))2 where Fcyl is the cylinder power and Î is the angle between the cylinder axis and the new meridian. It is also easy to remember the major angles 30º, 45º, 60º, and 90º as 25%, 50%, 75%, and 100% of the cylinder power respectively.
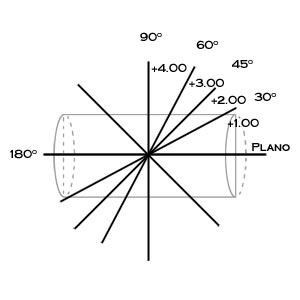
Since a spherical curve is the same in all meridians, if a -2.00 D spherical curve is combined with a +4.00 D cylinder at 45º, we end up with a compound lens described by the power cross below.
These curves on the lens surface can easily be measured with an instrument called a lens measure or lens clock.
A lens measure has three points of contact which are placed on the lens surface to measure its curve. The outer two points are stationary while the inner point moves in or out to measure the sagittal depth of the lens. From the sagittal depth the instrument indicator displays the curve in diopters, with plus (+) curves shown in one direction and minus (-) curves in the other. The lens measure can also be used to determine whether a lens surface is spherical or toric by placing the lens measure on the optical center of a lens and rotating the instrument about the center. If the indicator does not move while rotating, the surface is spherical. If the indicator changes when the lens measure is rotated, the lens surface is toric, with the minimum and maximum readings corresponding to the meridians of power.
When using a lens measure, keep in mind the instrument is calibrated to read powers of lens materials with a refractive index of 1.53, therefore higher index materials will have a true power greater than the indicated measurement.
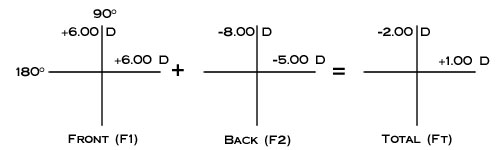
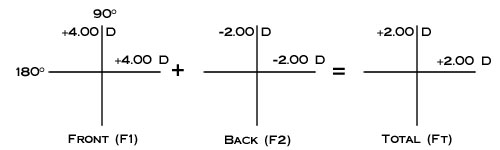
With a lens measure, the power cross, and the total power equation (F1 + F2 = FTotal) it is possible to determine the nominal power of spherical and toric lenses. For example, if we use the lens measure to find the curve on the front surface of a lens to be +4.00 D in all meridians and the curve on the back surface of the same lens to be -2.00 D in all meridians, we know the curves are spherical and can determine the total power of the lens as follows:
 Â
Â
Now, if we find the curve on the front surface of the lens to be +6.00 D and determine the back surface to be toric with a measurement of -8.00 D in the 90º meridian and -5.00 in the 180º meridian our power determination would look like this: